多孔構造体のポアソン比は空孔配列の差に敏感に応答 7) することが推定される ajお よびbjが 決まると一般にνj*が求められる モデルA, Bについて例としてν0=0, 03, 05の場 合を示す (Fig 4(a)~(c)) この図からモデルA, B比は,05 に近いことが多く(045~049),ポアソン比の値 的には,流体に近いことが分かる.このことからも,軟弱 地盤は揺れやすいことが理解できる.なお,コンクリート はν=1/6~1/12 程度,スチールはν=1/3~1/4 程度,岩石は 025,程度である. (4)密度:ρポアソン比 線膨張係数(1/℃) 鉄筋 5 x 10 51 x 105 コンクリート 335 x 10 4 x (γ/24) 2 x (Fc/60) 1/3 02 1 x 105 例) Fc = 21 N/mm 2 ヤング率 = 335 x 104 x {(241)/24}2 x (21/60)1/3 = 21,862 (N/mm 2) コンクリートの許容応力度 (N/mm 2 ) 長期 短期 圧縮 引張 せん断 圧縮 引張 せん断 普通コンクリート
ポアソン比nとは 技術士 建設部門 土質及び基礎 のブログ
ポアソン比0 5以上
ポアソン比0 5以上-下記にポアソン比の値を示します。 ・コンクリート 02、1/6=0167 ・鋼 030 ポアソン比の詳細は下記が参考になります。 ポアソン比の基礎知識、縦弾性係数との関係 まとめ 今回はポアソン比の記号について説明しました。ポアソン比の記号はν(にゅー · ポアソン比が0というのは、縦にのばしても幅が縮まずに膨張してくれる(密度が下がって変形してくれる)物質です。 ポアソン比の最大値は、膨張してくれずに体積が一定のまま(重量一定なので密度も一定のまま)の物質です。この場合 ます。 弾性領域




ポアソン比とは 世界一簡単にポアソン比がわかるページ プロダクトデザインのやさしい教科書
· ポアソン比νの値は、0≦ν≦05の範囲となります。 無次元の歪の比率ですから、ポアソン比も無次元で、単位は有りません。 ポアソン比は体積変化しやすさを示す数値でもある小ポアソン比はxy方向:nuxy、yz方向:nuyz、xz方向:nuxzとなります。 ansysでは05以上、および10以下のポアソン比は入力できません。 関連用語 ポアソン比、 小ポアソン比 cae用語辞典の転載・複製・引用・リンクなどについては、「著作権についてのお願い」をご確認ください。 contactQ w =05 p K z < v x Ý Ë w M v T > =1 p K { \ w P t m M o G T s Ã Í t Ô b { «) u Q p y V p x6 Ø T y ¹ C ` h Ý 6 p w p K w p z \ \ p w A L(1 M ² ¹ C) q x s { ~ Ù ¹ ï z =05( y V P) 2 1=0 u !
ポアソン比の上限は理論的に05となりますが、この ポアソン比が05 というのは 体積が一定 であることを意味します。 普通、材料は圧縮されると体積が減りますが、 ポアソン比が05の材料は圧縮時にも体積が減りません 。ポアソン比が最も高い材料はどれですか? ゴムのポアソン比は最も高く、ほぼ05に相当します。 ポアソン比が常に正であるのはなぜですか? ポアソン比は、横ひずみと軸ひずみの比の負の値です。 伸びは直径の収縮を引き起こし、最終的に比率を負にする上の表で求めた断面力は、ポアソン比をν=0とした場合の値である。 そこで、入力したν=00に対する値を次式を用いて補正する。 なお、νによる補正は、版の中央で直交するMx2とMy2に対して行う。 ここに、 ν1補正前のポアソン比= 0000 ν2実際のポアソン比(入力値)= 00 Mx2,My2補正前の
· 生体のポアソン比の求め方(ポアソン比が0.5を証明する) 学校の授業でポアソン比の問題がでました。 「生体のポアソン比は0.5であるのを証明する。 生体の体積は一定。ひずみは全体の大きさに対して非常に小さい」 「生体」とは何か具体的には決まってません。 そして「生体」は円柱として考えてもいいとのことです。 「ひずみは全体の大きさに対しAnsysではポアソン比は PRXY と略して記載されます。(等方性材料の場合) 直交異方性材料における取り扱いは、「大ポアソン比」および「小ポアソン比」の項目をご覧ください。 Ansysでは05以上、および10以下のポアソン比は入力できません。 関連用語(3)伸 度(常 温伸長による)の 増加とともに,各 伸度レベルにおけるポアソン比は減少する。 (4)低 延伸領域(延 伸率25倍 以下)で はポアソン比が05よ り大きな値を示し,高延伸領域(延 伸率30倍 以上)で は反対に05よ り小さな値を示す




05 号 見かけのポアソン比の制御構造 見かけのポアソン比制御方法およびそれを使用したセンサまたは装置 Astamuse




2 37 非金属材料 Monozukuri Hitozukuri 日本のものづくり
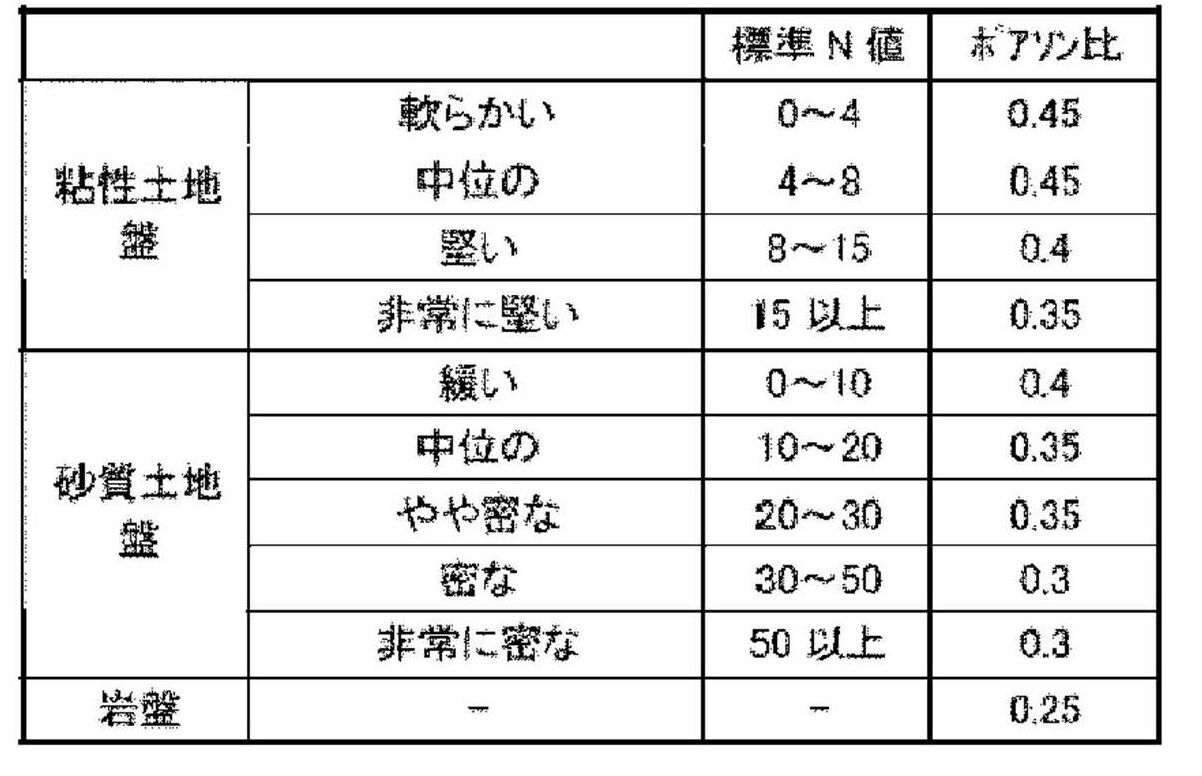
負のポアソン比,熱弾粘塑性ツースケール解析 損傷解析,弾粘塑性トリプルスケール解析 均質化法について Microscopic ユニットセル問題 , i kl F i M :特性関数,, ( ) kl ij ijpq pk ql q klp ijkl kl lk cE c F M V G G E 微視的発展式 Macroscopic ,, ( ) kl ij ijpq pk ql q klp ijkl kl lk cE c F M 6 G G E 巨視的関係式2404 · ポアソン比を求めるには、物体を伸ばしたときや圧縮したときの変化量(⊿lと⊿d)を調べる必要があります。 ・伸び縮みした長さを(⊿l) ・伸び縮みによって発生した径方向の変化量を(⊿d)で表します。 ポアソン比の計算式は下記の通りです。表-3は申(19)5)がHobst and Zajic(19)6)の岩 石の変形係数,ポアソン比をまとめたものである。この 表は岩石の種類,風化度合いに応じてポアソン比を提示 しているので,解析者には利用しやすいと思われる。




2 37 非金属材料 Monozukuri Hitozukuri 日本のものづくり




ポアソン比nとは 技術士 建設部門 土質及び基礎 のブログ
· ポアソン分布の意味と平均・分散 レベル 大学数学その2 アクチュアリー 更新日時 ポアソン分布とは 「一定時間内にランダムなイベントが何回発生するか」 を表す分布です。 この記事では, ポアソン分布の意味 , ポアソン分布の式の導出 · ポアソンの式の導出および比熱比の値について解説します。 目次 状態方程式の微分 断熱変化であることを使う 比熱比と自由度 状態方程式の微分 以下, P P P は圧力, V V V は体積, n n n は気体のモル数, R R R は気体定数, T T T は絶対温度とします。 ポアソンの式の導出(前半)1105 · 各物質のポアソン比を見てみましょう。 ゴムが05と高くて、コルクがほぼ0であることを除けばだいたい 03~04程度 に集中していることが分かります。
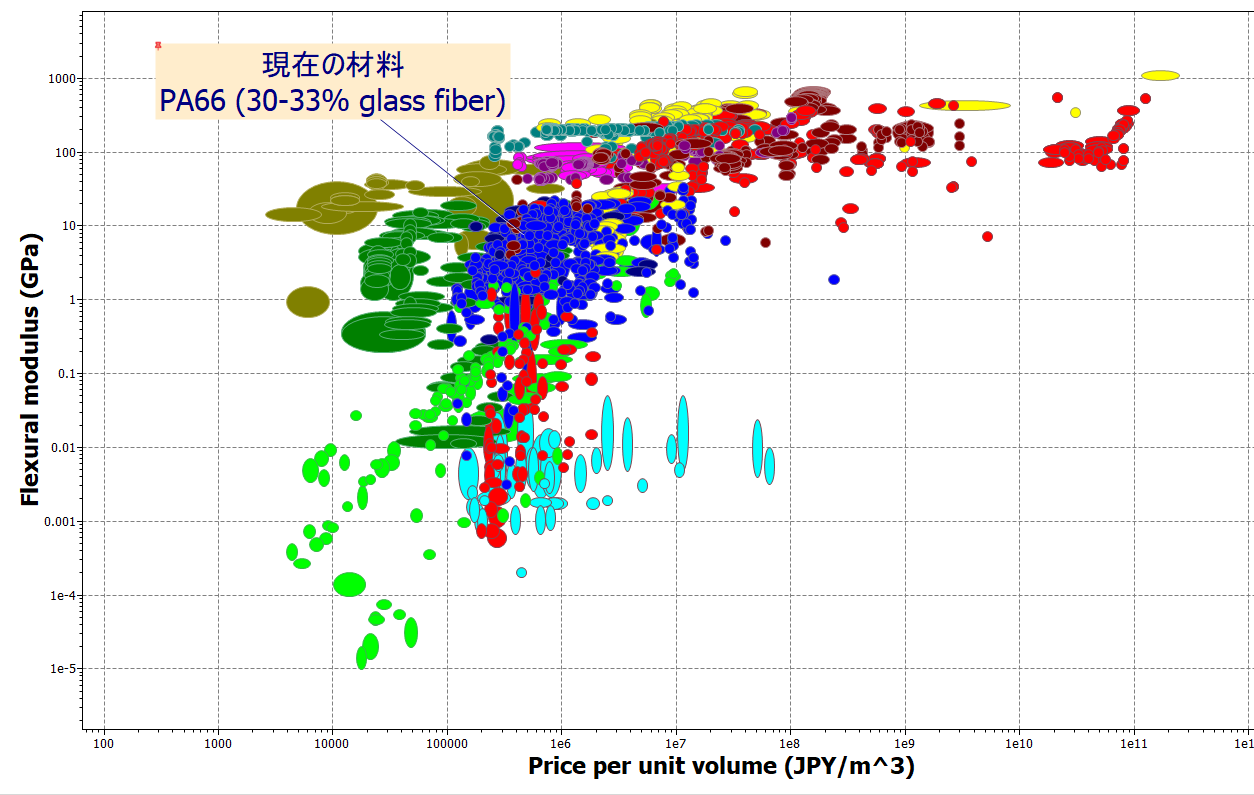



Pa66 ナイロン 66 とその代替材料の物性値 特性について 有限要素法マルチフィジックス解析ツール Ansys サイバネット
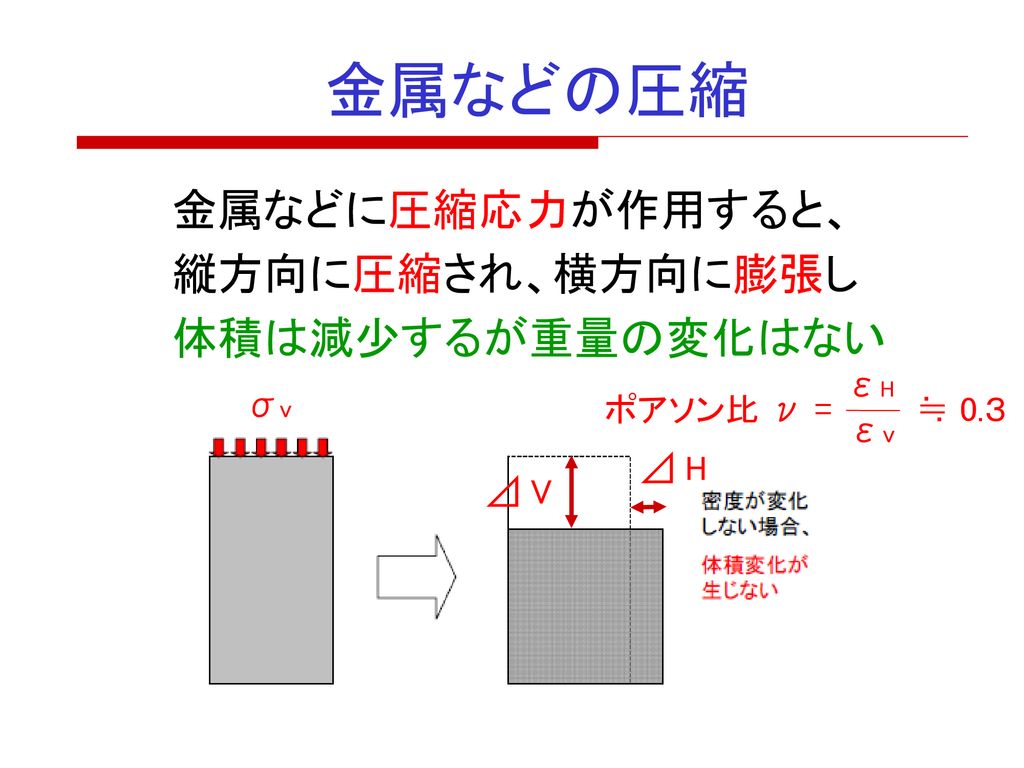



土質 基礎構造 6回目の授業 粘土の圧密 Consolidation 平成31年 5月20日 月 今岡 克也 Ppt Download
3材齢12 時間以降のポアソン比は,ほぼ一定となることが示された. 4どの材齢においてもひずみゲージから得られたポアソン比は,コンプレッソメーターよりも005 程度大き くなることが示された.2865であり、ほぼ05 に等しくなる。ポアソン比が05 であるということは、材料 は非圧縮(体積変化しない)ということである。 まとめると、ゴムは非常に小さい力で引き伸ばすことができるが、圧縮する には非常に大きい力を必要とする。すなわち、変形による面圧の大きさが工業 的な利点でここで、もし「力を加えた前後で体積がまったく変わらない」という仮定――非常に可塑性の高い、たとえば水のようなものを考える――を立てて計算してみるとポアソン比は約 05 になる。 この値がポアソン比の最大値です。 どうしてこんな話を始めたのかというと、このポアソン比という値が「剪断力と剪断変形」を考える上で重要になるからです。 下にある




2 37 非金属材料 Monozukuri Hitozukuri 日本のものづくり




ポアソン比とは 世界一簡単にポアソン比がわかるページ プロダクトデザインのやさしい教科書
· ・ポアソン比 02 ・線膨張係数 1×105 (1/℃) ※鋼材と同じ値である。 ※r:コンクリートの気乾単位体積重量(kN/m3) Fc:コンクリートの設計基準強度(N/㎜2) 鉄筋コンクリートの単位体積重量 ・普通コンクリート Fc≦36 240(kN/m3)95%信頼区間 下限:β 3L = 上限:β 3U = 尤度比検定 回帰の検定:χ β 2 =2251(p=052)<χ 2 (3,005)=7815 有意水準5%で有意ではない ズレの検定:χ LOF 2 =137(p=)<χ 2 (39,005)= 有意水準5%で有意ではない 図1521は横軸をポアソン回帰式から求めたl=ln(λ)の値にし、縦軸を= Á ` ~ =03( ° ` ï P) 2 1=04 ÀV'=(104 )V
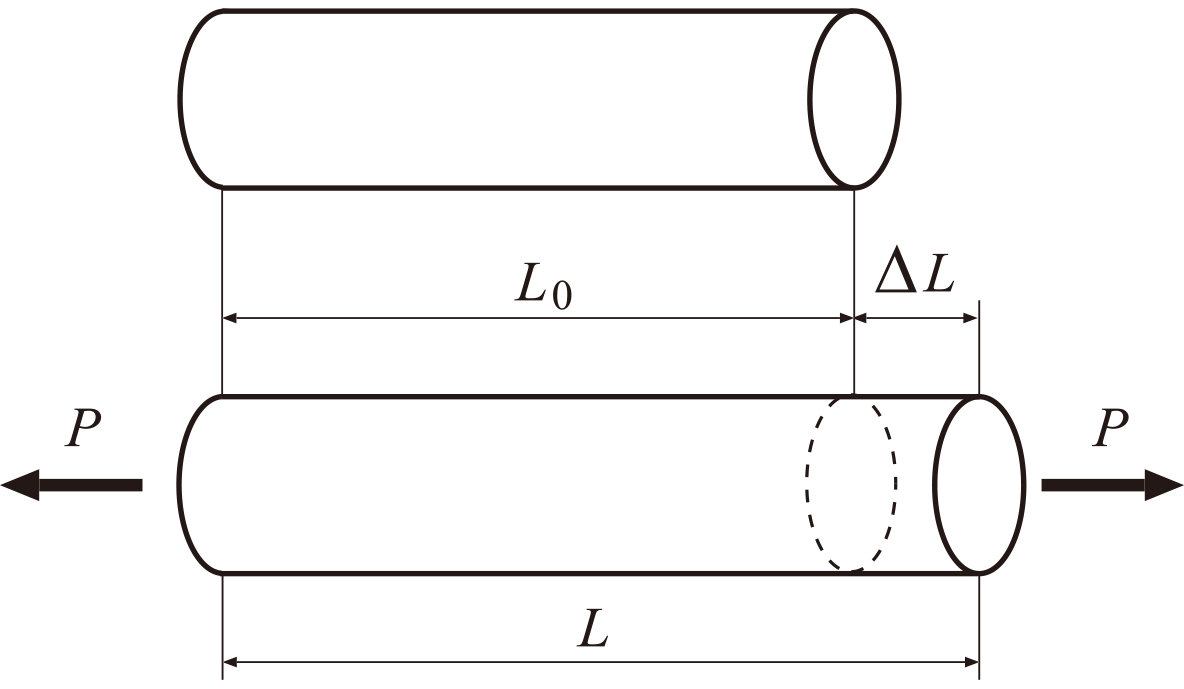



第1回 応力とひずみ 日本機械学会誌
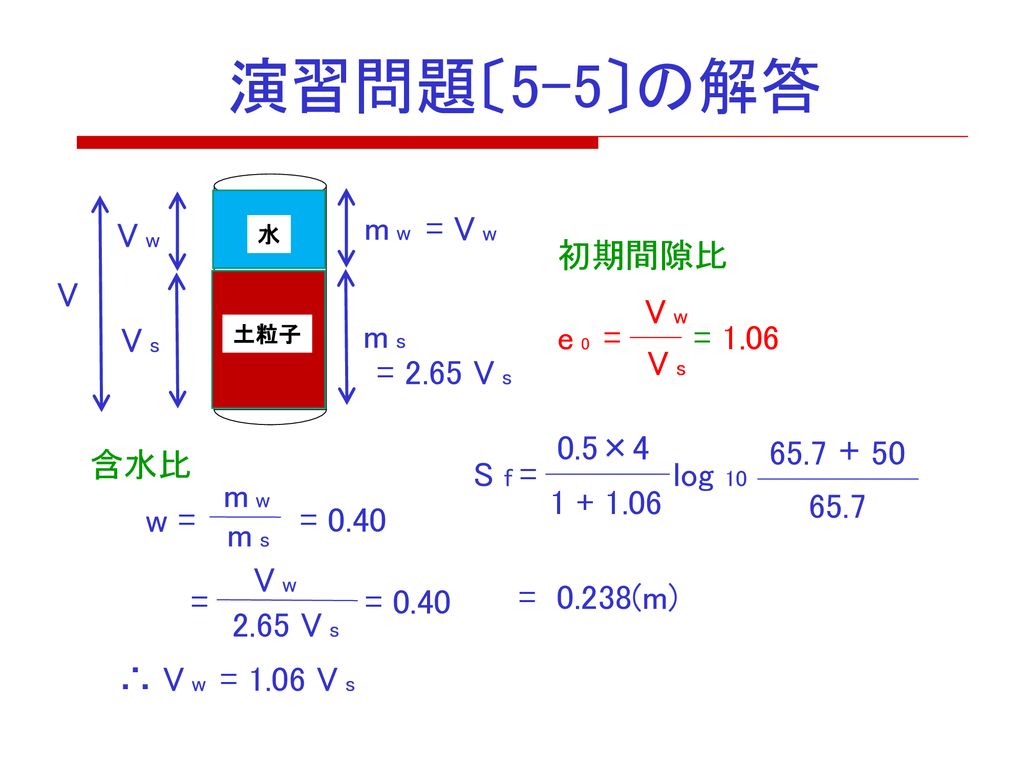



土質 基礎構造 6回目の授業 粘土の圧密 Consolidation 平成31年 5月20日 月 今岡 克也 Ppt Download
での縦ひずみに対する横ひずみの比によりポアソン比 を,1/3 圧縮強度範囲での縦ひずみに対する圧縮応力の 比によりヤング率を,最小二乗近似を用いて算出した。 24 密度試験および含水率測定 材齢05,075,1, 3, 7, 28日にて,封緘中のセ · ポアソン比 ポアソン比の範囲 材料が等方性の場合、単位体積当たりのひずみエネルギーであるひずみエネルギ関数 u0 は以下のように示される4。 u 0 = e ν 2 ( 1 &
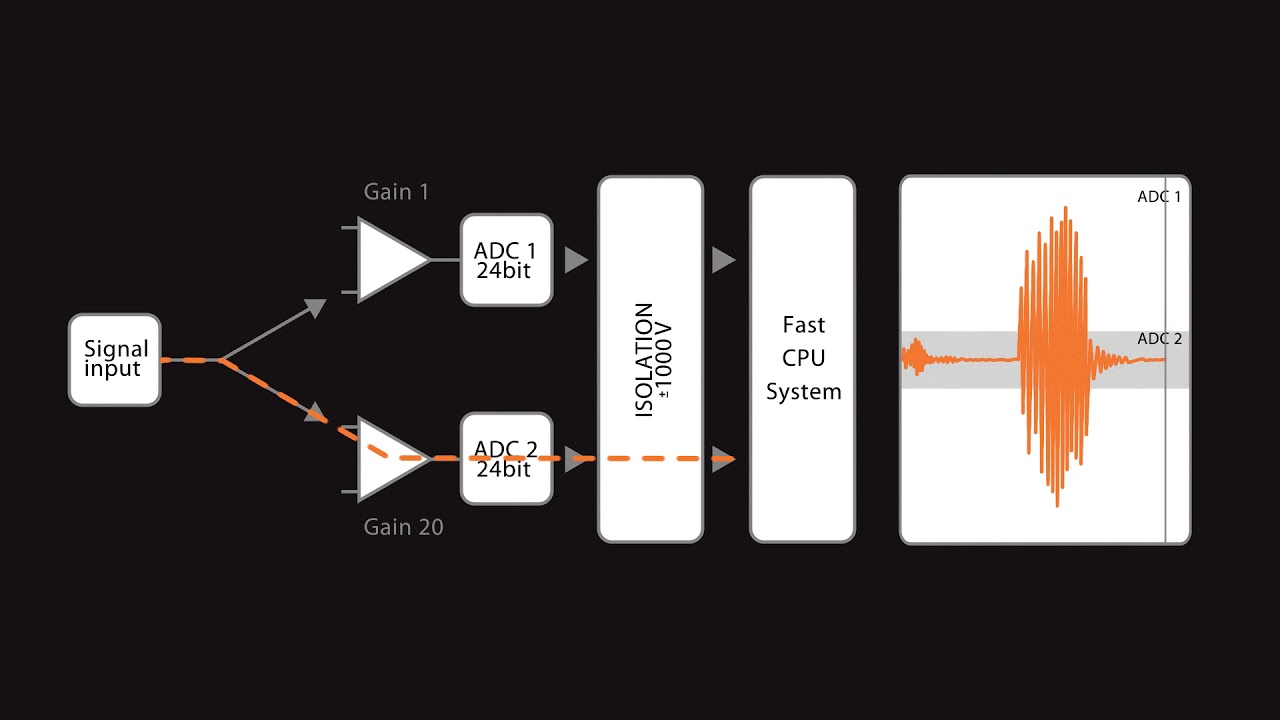



計測マメ知識 ひずみと圧力を計測する方法 デュージャパン株式会社




05 号 見かけのポアソン比の制御構造 見かけのポアソン比制御方法およびそれを使用したセンサまたは装置 Astamuse




ポアソン比とは 世界一簡単にポアソン比がわかるページ プロダクトデザインのやさしい教科書
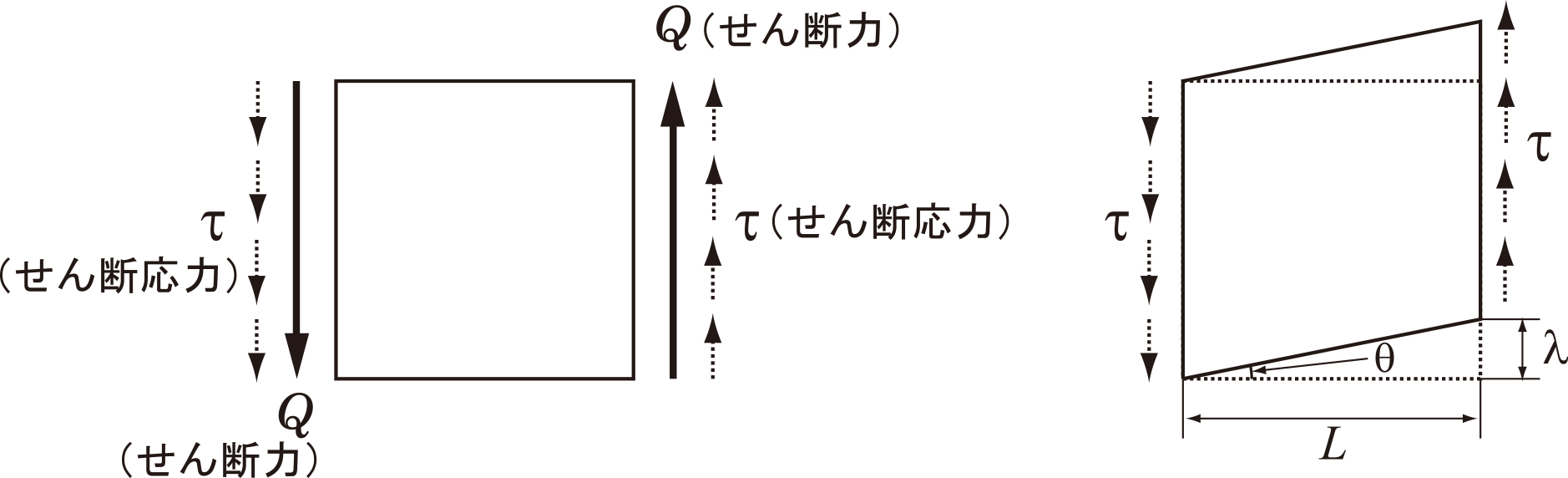



第1回 応力とひずみ 日本機械学会誌




Pdf Fundamentals And Applications Of Elasticity In Composite Materials Elastic Wave Propagation In Anisotropic Rocks In Japanese
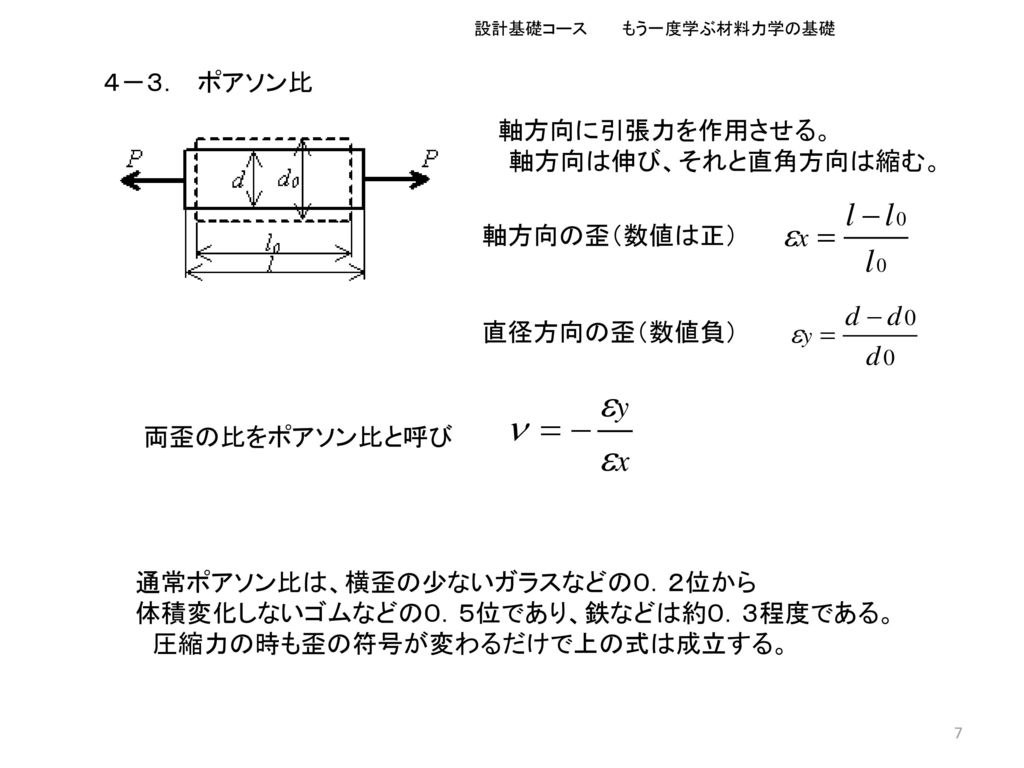



設計基礎コース もう一度学ぶ材料力学の基礎 Ppt Download




Pdf Inside Story Of A Protein Molecule As Reported By Fracture Mechanics




長さの違う柱が2本ある材料力学の問題について Okwave



Solid Mechanics
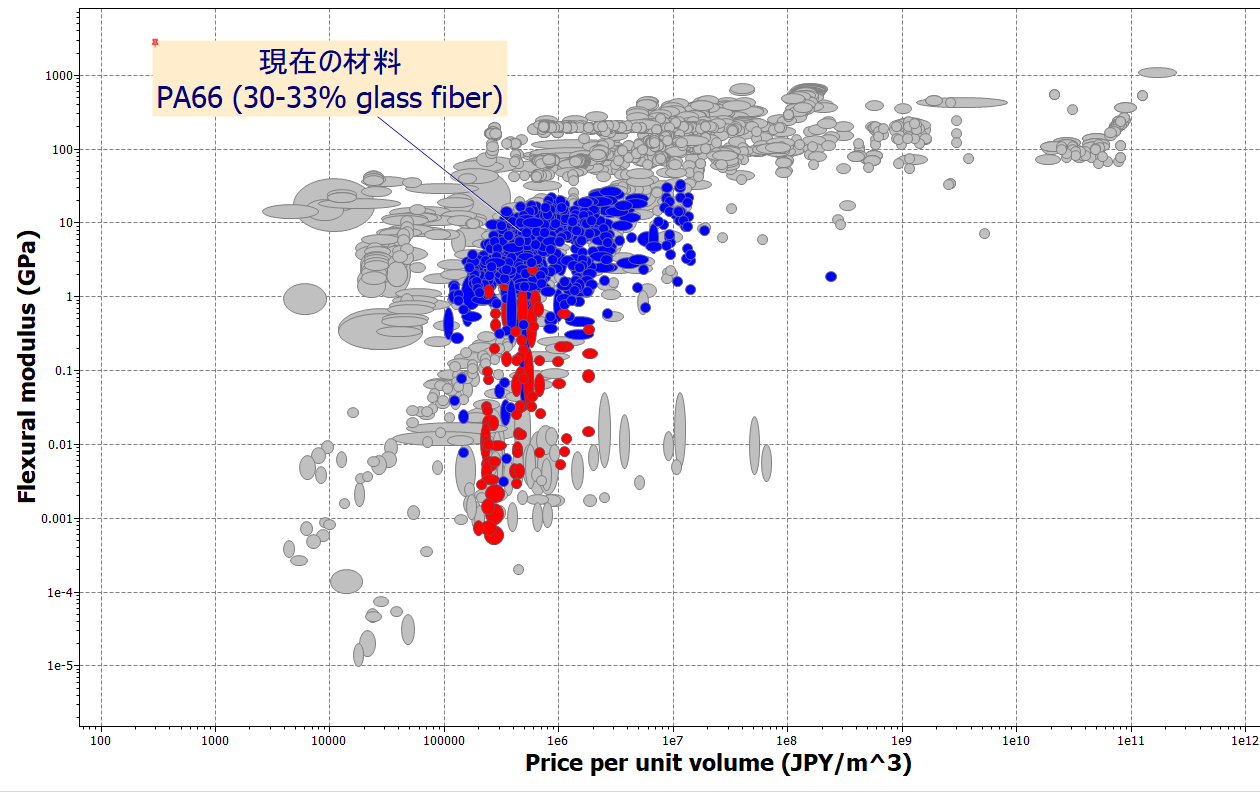



Pa66 ナイロン 66 とその代替材料の物性値 特性について 有限要素法マルチフィジックス解析ツール Ansys サイバネット
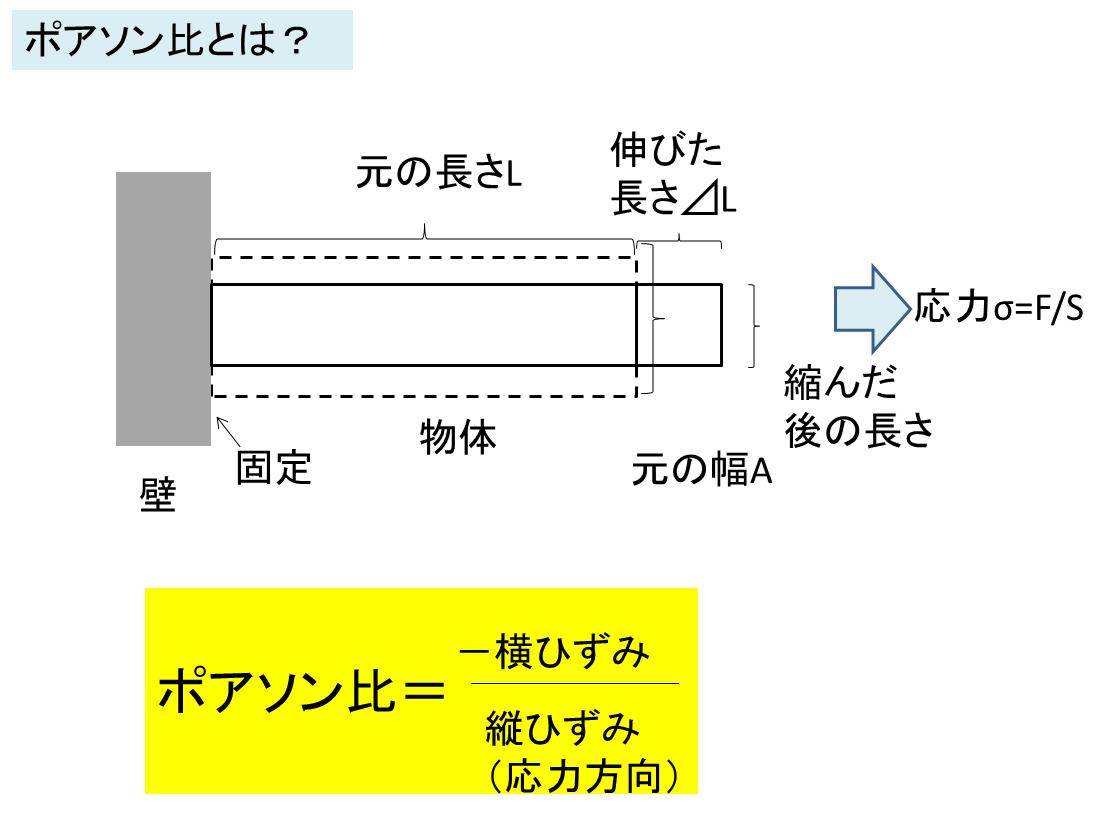



材料力学 ポアソン比とは 求め方と使用方法 リチウムイオン電池の構造解析



21年版 引張試験機5選 製造メーカー14社一覧 メトリー
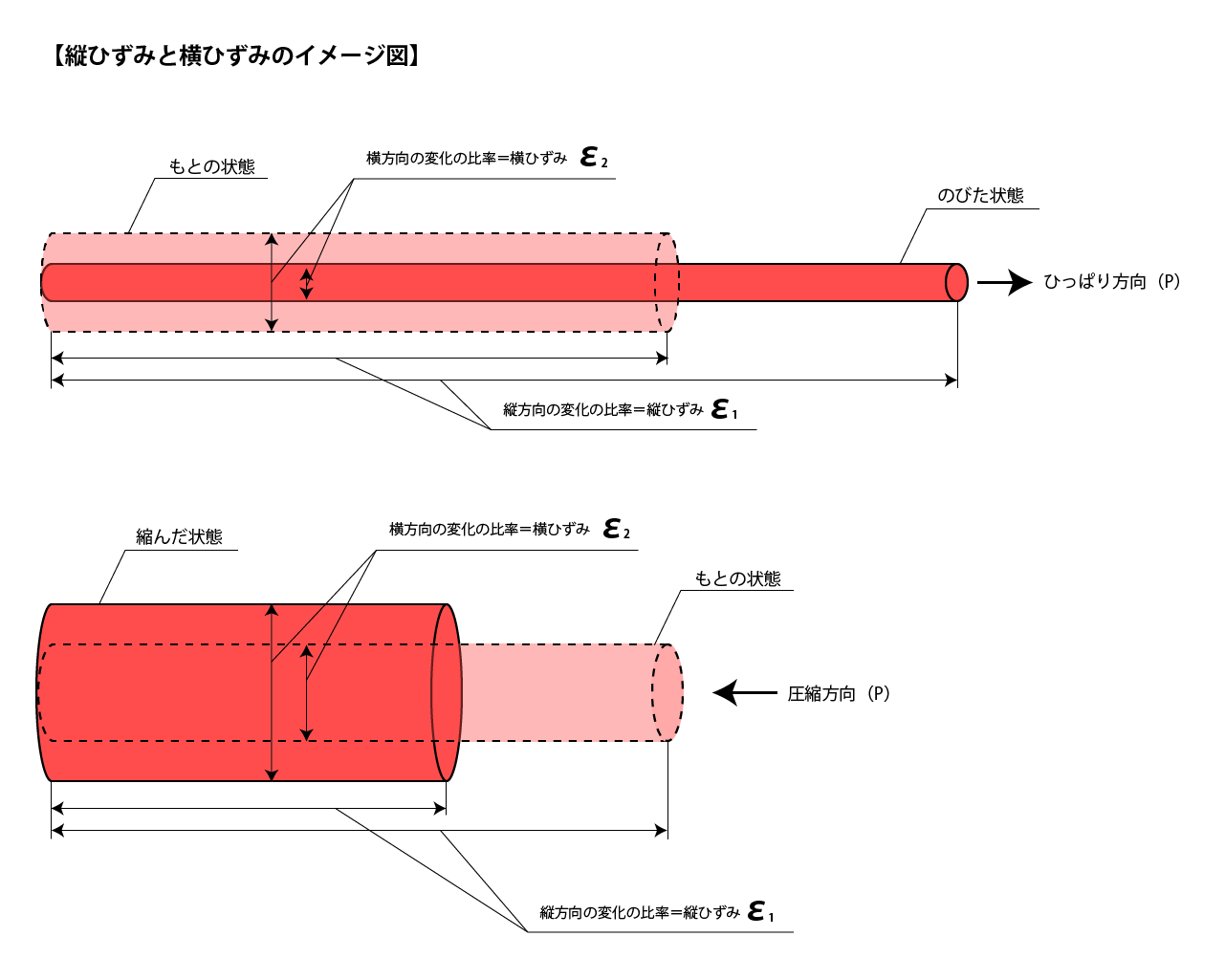



ポアソン比とは 世界一簡単にポアソン比がわかるページ プロダクトデザインのやさしい教科書




複雑な形状の円型の管における体積の計算の仕方 Okwave
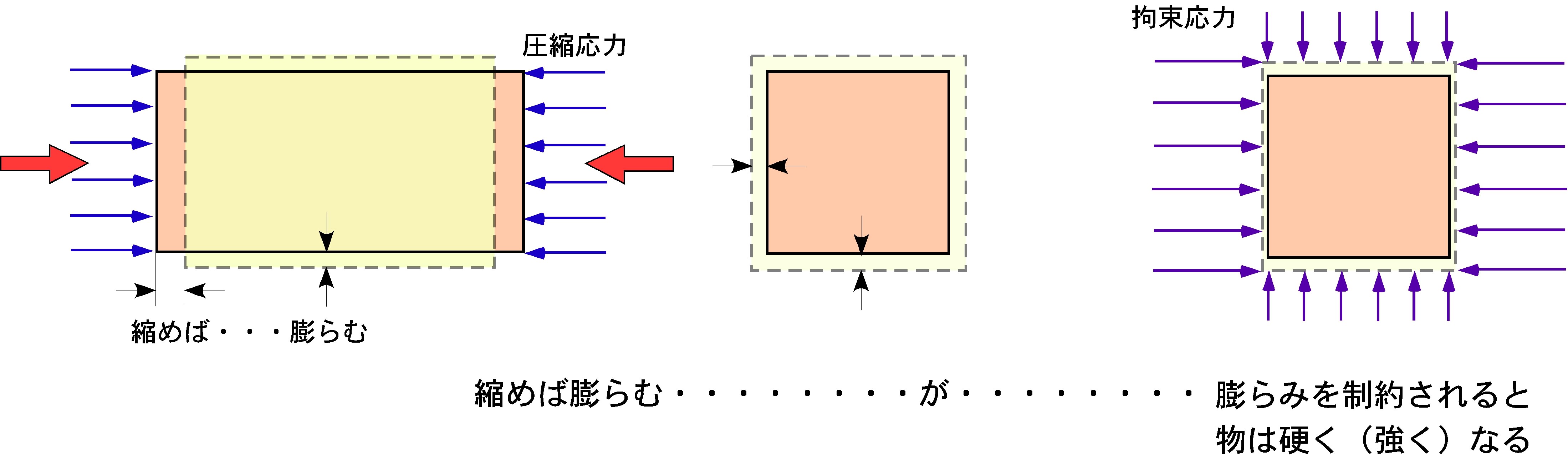



正断層の余震について 続 ガリレオ爺さんのブログ



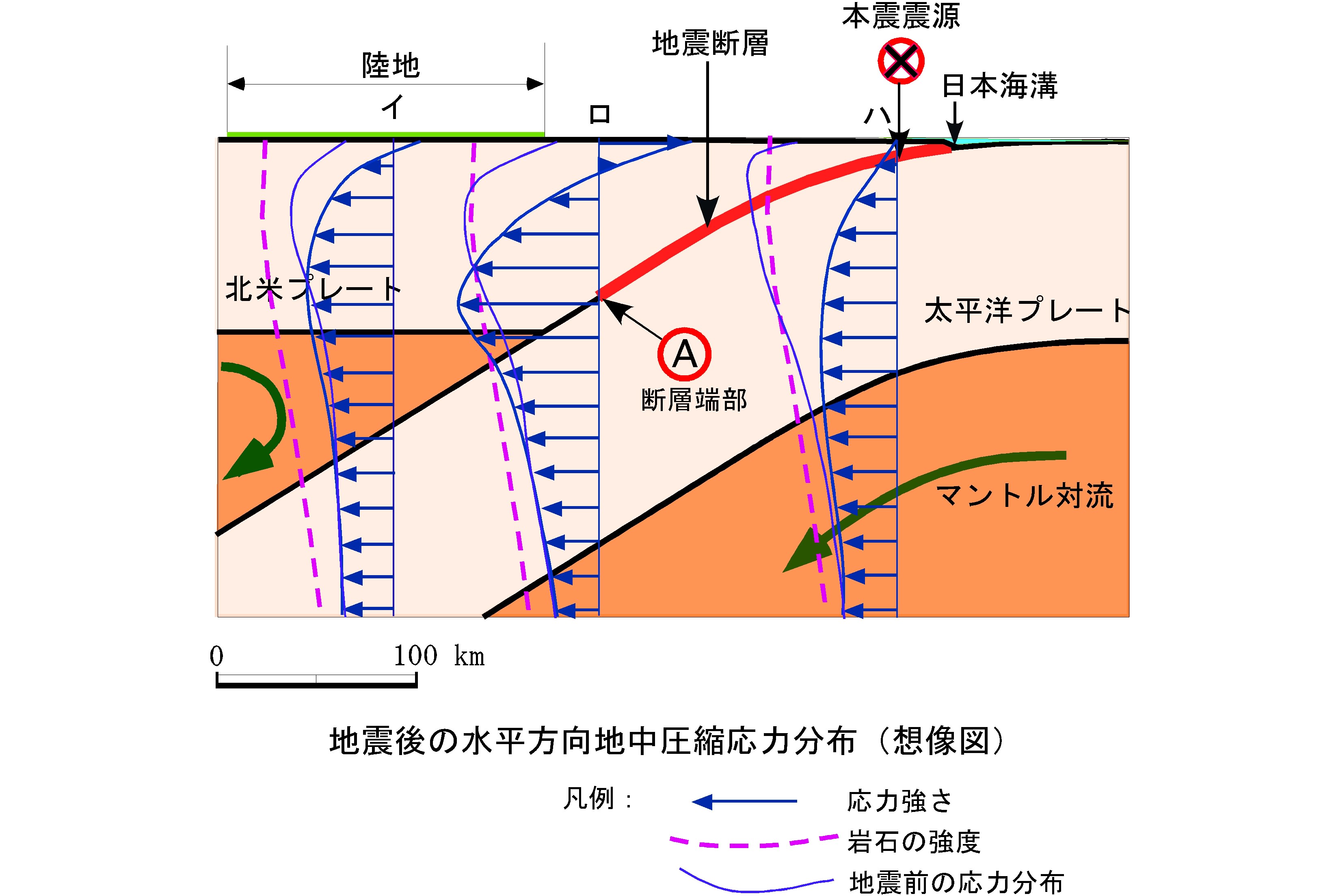
平成23年 11年 東北地方太平洋沖地震 地震予知研究センター



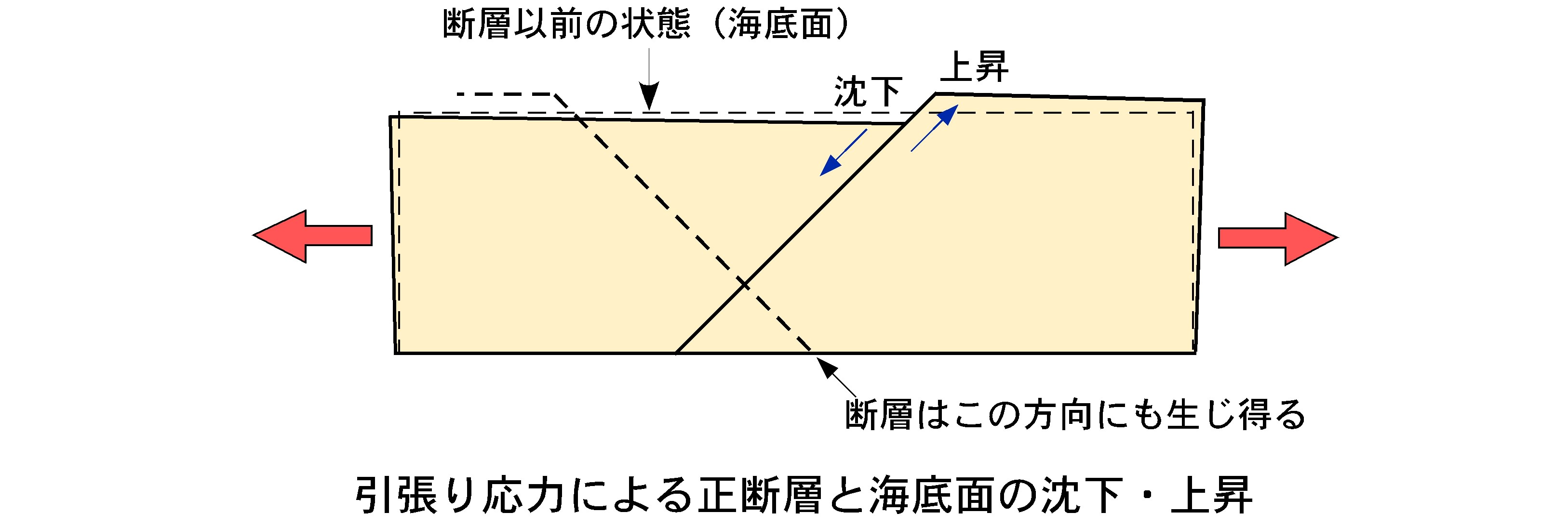
正断層の余震について 続 ガリレオ爺さんのブログ




05 号 見かけのポアソン比の制御構造 見かけのポアソン比制御方法およびそれを使用したセンサまたは装置 Astamuse




21年版 引張試験機5選 製造メーカー14社一覧 メトリー



正断層の余震について 続 ガリレオ爺さんのブログ
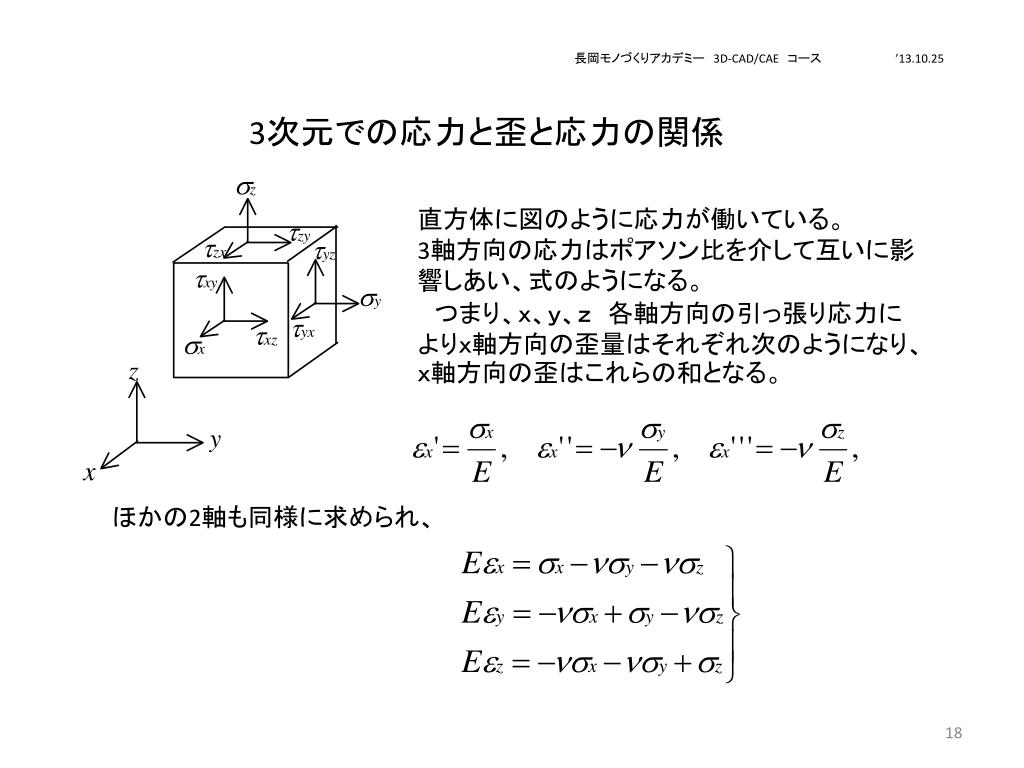



Ppt 長岡モノづくりアカデミー 3d Cad Cae コース 13 10 25 Powerpoint Presentation Id
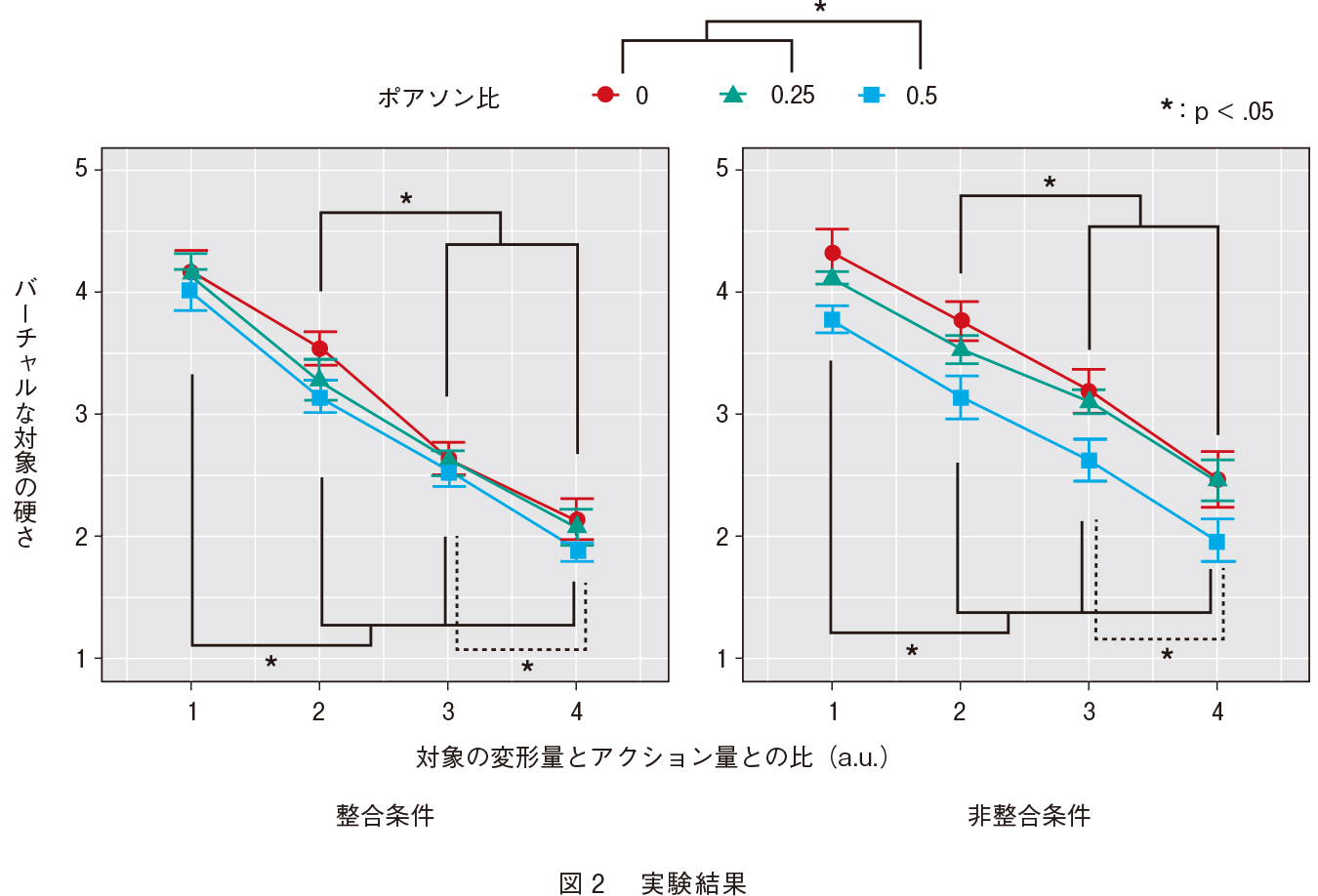



空中擬似触覚による質感提示をめざして Ntt技術ジャーナル




05 号 見かけのポアソン比の制御構造 見かけのポアソン比制御方法およびそれを使用したセンサまたは装置 Astamuse




05 号 見かけのポアソン比の制御構造 見かけのポアソン比制御方法およびそれを使用したセンサまたは装置 Astamuse



21年版 引張試験機5選 製造メーカー14社一覧 メトリー




Pdf Modeling And Crystal Plasticity Analysis Of Multiple Slip Deformation In The Microstructure Of Particle Dispersed Alloy And Its Macroscopic Strain Hardening Characteristics



No comments:
Post a Comment